#NBVAL_IGNORE_OUTPUT
%reset -f
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline08 - Snapshotting with Devito using the ConditionalDimension
This notebook intends to introduce new Devito users (especially with a C or FORTRAN background) to the best practice on saving snapshots to disk, as a binary float file.
We start by presenting a naive approach, and then introduce a more efficient method, which exploits Devito’s ConditionalDimension.
Initialize utilities
Problem Setup
This tutorial is based on an example that has appeared in a TLE tutorial(Louboutin et. al., 2017), in which one shot is modeled over a 2-layer velocity model.
# This cell sets up the problem that is already explained in the first TLE tutorial.
#NBVAL_IGNORE_OUTPUT
#%%flake8
from examples.seismic import Receiver
from examples.seismic import RickerSource
from examples.seismic import Model, plot_velocity, TimeAxis
from devito import TimeFunction
from devito import Eq, solve
from devito import Operator
# Set velocity model
nx = 201
nz = 201
nb = 10
shape = (nx, nz)
spacing = (20., 20.)
origin = (0., 0.)
v = np.empty(shape, dtype=np.float32)
v[:, :int(nx/2)] = 2.0
v[:, int(nx/2):] = 2.5
model = Model(vp=v, origin=origin, shape=shape, spacing=spacing,
space_order=2, nbl=10, bcs="damp")
# Set time range, source, source coordinates and receiver coordinates
t0 = 0. # Simulation starts a t=0
tn = 1000. # Simulation lasts tn milliseconds
dt = model.critical_dt # Time step from model grid spacing
time_range = TimeAxis(start=t0, stop=tn, step=dt)
nt = time_range.num # number of time steps
f0 = 0.010 # Source peak frequency is 10Hz (0.010 kHz)
src = RickerSource(
name='src',
grid=model.grid,
f0=f0,
time_range=time_range)
src.coordinates.data[0, :] = np.array(model.domain_size) * .5
src.coordinates.data[0, -1] = 20. # Depth is 20m
rec = Receiver(
name='rec',
grid=model.grid,
npoint=101,
time_range=time_range) # new
rec.coordinates.data[:, 0] = np.linspace(0, model.domain_size[0], num=101)
rec.coordinates.data[:, 1] = 20. # Depth is 20m
depth = rec.coordinates.data[:, 1] # Depth is 20m
plot_velocity(model, source=src.coordinates.data,
receiver=rec.coordinates.data[::4, :])
#Used for reshaping
vnx = nx+20
vnz = nz+20
# Set symbolics for the wavefield object `u`, setting save on all time steps
# (which can occupy a lot of memory), to later collect snapshots (naive method):
u = TimeFunction(name="u", grid=model.grid, time_order=2,
space_order=2, save=time_range.num)
# Set symbolics of the operator, source and receivers:
pde = model.m * u.dt2 - u.laplace + model.damp * u.dt
stencil = Eq(u.forward, solve(pde, u.forward))
src_term = src.inject(field=u.forward, expr=src * dt**2 / model.m)
rec_term = rec.interpolate(expr=u)
op = Operator([stencil] + src_term + rec_term, subs=model.spacing_map)
# Run the operator for `(nt-2)` time steps:
op(time=nt-2, dt=model.critical_dt)Operator `initdamp` run in 0.01 s
Operator `padfunc` run in 0.01 s
Operator `Kernel` run in 0.03 s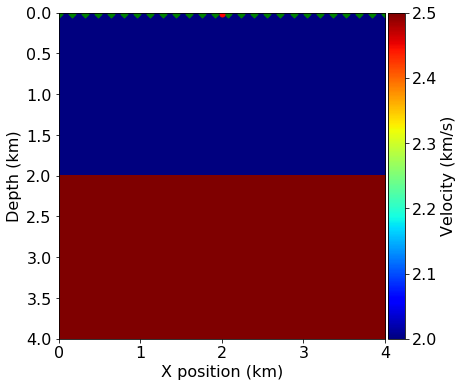
PerformanceSummary([(PerfKey(name='section0', rank=None),
PerfEntry(time=0.02613699999999999, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section1', rank=None),
PerfEntry(time=0.0007910000000000022, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section2', rank=None),
PerfEntry(time=0.0010599999999999995, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[]))])Saving snaps to disk - naive approach
We want to get equally spaced snaps from the nt-2 saved in u.data. The user can then define the total number of snaps nsnaps, which determines a factor to divide nt.
nsnaps = 100
factor = round(u.shape[0] / nsnaps) # Get approx nsnaps, for any nt
ucopy = u.data.copy(order='C')
filename = "naivsnaps.bin"
file_u = open(filename, 'wb')
for it in range(0, nsnaps):
file_u.write(ucopy[it*factor, :, :])
file_u.close()Checking u.data spaced by factor using matplotlib,
#NBVAL_IGNORE_OUTPUT
plt.rcParams['figure.figsize'] = (20, 20) # Increases figure size
imcnt = 1 # Image counter for plotting
plot_num = 5 # Number of images to plot
for i in range(0, nsnaps, int(nsnaps/plot_num)):
plt.subplot(1, plot_num+1, imcnt+1)
imcnt = imcnt + 1
plt.imshow(np.transpose(u.data[i * factor, :, :]), vmin=-1, vmax=1, cmap="seismic")
plt.show()
Or from the saved file:
#NBVAL_IGNORE_OUTPUT
fobj = open("naivsnaps.bin", "rb")
snaps = np.fromfile(fobj, dtype = np.float32)
snaps = np.reshape(snaps, (nsnaps, vnx, vnz)) #reshape vec2mtx, devito format. nx first
fobj.close()
plt.rcParams['figure.figsize'] = (20,20) # Increases figure size
imcnt = 1 # Image counter for plotting
plot_num = 5 # Number of images to plot
for i in range(0, nsnaps, int(nsnaps/plot_num)):
plt.subplot(1, plot_num+1, imcnt+1);
imcnt = imcnt + 1
plt.imshow(np.transpose(snaps[i,:,:]), vmin=-1, vmax=1, cmap="seismic")
plt.show() 
This C/FORTRAN way of saving snaps is clearly not optimal when using Devito; the wavefield object u is specified to save all snaps, and a memory copy is done at every op time step. Giving that we don’t want all the snaps saved, this process is wasteful; only the selected snapshots should be copied during execution.
To address these issues, a better way to save snaps using Devito’s capabilities is presented in the following section.
Saving snaps to disk - Devito method
A better way to save snapshots to disk is to create a new TimeFunction, usave, whose time size is equal to nsnaps. There are 3 main differences from the previous code, which are flagged by #Part 1, #Part 2 and #Part 3 . After running the code each part is explained with more detail.
#NBVAL_IGNORE_OUTPUT
from devito import ConditionalDimension
nsnaps = 103 # desired number of equally spaced snaps
factor = round(nt / nsnaps) # subsequent calculated factor
print(f"factor is {factor}")
#Part 1 #############
time_subsampled = ConditionalDimension(
't_sub', parent=model.grid.time_dim, factor=factor)
usave = TimeFunction(name='usave', grid=model.grid, time_order=2, space_order=2,
save=nsnaps, time_dim=time_subsampled)
print(time_subsampled)
#####################
u = TimeFunction(name="u", grid=model.grid, time_order=2, space_order=2)
pde = model.m * u.dt2 - u.laplace + model.damp * u.dt
stencil = Eq(u.forward, solve(pde, u.forward))
src_term = src.inject(
field=u.forward,
expr=src * dt**2 / model.m)
rec_term = rec.interpolate(expr=u)
#Part 2 #############
op1 = Operator([stencil] + src_term + rec_term,
subs=model.spacing_map) # usual operator
op2 = Operator([stencil] + src_term + [Eq(usave, u)] + rec_term,
subs=model.spacing_map) # operator with snapshots
op1(time=nt - 2, dt=model.critical_dt) # run only for comparison
u.data.fill(0.)
op2(time=nt - 2, dt=model.critical_dt)
#####################
#Part 3 #############
print("Saving snaps file")
print("Dimensions: nz = {:d}, nx = {:d}".format(nz + 2 * nb, nx + 2 * nb))
filename = "snaps2.bin"
usave.data.tofile(filename)
#####################factor is 2
t_sub
Saving snaps file
Dimensions: nz = 221, nx = 221Operator `Kernel` run in 0.02 s
Operator `Kernel` run in 0.03 sAs usave.data has the desired snaps, no extra variable copy is required. The snaps can then be visualized:
#NBVAL_IGNORE_OUTPUT
fobj = open("snaps2.bin", "rb")
snaps = np.fromfile(fobj, dtype=np.float32)
snaps = np.reshape(snaps, (nsnaps, vnx, vnz))
fobj.close()
plt.rcParams['figure.figsize'] = (20, 20) # Increases figure size
imcnt = 1 # Image counter for plotting
plot_num = 5 # Number of images to plot
for i in range(0, plot_num):
plt.subplot(1, plot_num, i+1);
imcnt = imcnt + 1
ind = i * int(nsnaps/plot_num)
plt.imshow(np.transpose(snaps[ind,:,:]), vmin=-1, vmax=1, cmap="seismic")
plt.show() 
About Part 1
Here a subsampled version (time_subsampled) of the full time Dimension (model.grid.time_dim) is created with the ConditionalDimension. time_subsampled is then used to define an additional symbolic wavefield usave, which will store in usave.data only the predefined number of snapshots (see Part 2).
Further insight on how ConditionalDimension works and its most common uses can be found in the Devito documentation. The following excerpt exemplifies subsampling of simple functions:
Among the other things, ConditionalDimensions are indicated to implement
Function subsampling. In the following example, an Operator evaluates the
Function ``g`` and saves its content into ``f`` every ``factor=4`` iterations.
>>> from devito import Dimension, ConditionalDimension, Function, Eq, Operator
>>> size, factor = 16, 4
>>> i = Dimension(name='i')
>>> ci = ConditionalDimension(name='ci', parent=i, factor=factor)
>>> g = Function(name='g', shape=(size,), dimensions=(i,))
>>> f = Function(name='f', shape=(int(size/factor),), dimensions=(ci,))
>>> op = Operator([Eq(g, 1), Eq(f, g)])
The Operator generates the following for-loop (pseudocode)
.. code-block:: C
for (int i = i_m; i <= i_M; i += 1) {
g[i] = 1;
if (i%4 == 0) {
f[i / 4] = g[i];
}
}From this excerpt we can see that the C code generated by Operator with the extra argument Eq(f,g) mainly corresponds to adding an if block on the optimized C-code, which saves the desired snapshots on f, from g, at the correct times. Following the same line of thought, in the following section the symbolic and C-generated code are compared, with and without snapshots.
About Part 2
We then define Operators op1 (no snaps) and op2 (with snaps). The only difference between the two is that op2 has an extra symbolic equation Eq(usave, u). Notice that even though usave and u have different Dimensions, Devito’s symbolic interpreter understands it, because usave’s time_dim was defined through the ConditionalDimension.
Below, we show relevant excerpts of the compiled Operators. As explained above, the main difference between the optimized C-code of op1 and op2 is the addition of an if block. For op1’s C code:
// #define's
//...
// declare dataobj struct
//...
// declare profiler struct
//...
int Kernel(struct dataobj *restrict damp_vec, const float dt, struct dataobj *restrict m_vec, const float o_x, const float o_y, struct dataobj *restrict rec_vec, struct dataobj *restrict rec_coords_vec, struct dataobj *restrict src_vec, struct dataobj *restrict src_coords_vec, struct dataobj *restrict u_vec, const int x_M, const int x_m, const int y_M, const int y_m, const int p_rec_M, const int p_rec_m, const int p_src_M, const int p_src_m, const int time_M, const int time_m, struct profiler * timers)
{
// ...
// ...
float (*restrict u)[u_vec->size[1]][u_vec->size[2]] __attribute__ ((aligned (64))) = (float (*)[u_vec->size[1]][u_vec->size[2]]) u_vec->data;
// ...
for (int time = time_m, t0 = (time)%(3), t1 = (time + 1)%(3), t2 = (time + 2)%(3); time <= time_M; time += 1, t0 = (time)%(3), t1 = (time + 1)%(3), t2 = (time + 2)%(3))
{
struct timeval start_section0, end_section0;
gettimeofday(&start_section0, NULL);
for (int x = x_m; x <= x_M; x += 1)
{
#pragma omp simd
for (int y = y_m; y <= y_M; y += 1)
{
float r0 = 1.0e+4F*dt*m[x + 2][y + 2] + 5.0e+3F*(dt*dt)*damp[x + 1][y + 1];
u[t1][x + 2][y + 2] = 2.0e+4F*dt*m[x + 2][y + 2]*u[t0][x + 2][y + 2]/r0 - 1.0e+4F*dt*m[x + 2][y + 2]*u[t2][x + 2][y + 2]/r0 + 1.0e+2F*((dt*dt*dt)*u[t0][x + 1][y + 2]/r0 + (dt*dt*dt)*u[t0][x + 2][y + 1]/r0 + (dt*dt*dt)*u[t0][x + 2][y + 3]/r0 + (dt*dt*dt)*u[t0][x + 3][y + 2]/r0) + 5.0e+3F*(dt*dt)*damp[x + 1][y + 1]*u[t2][x + 2][y + 2]/r0 - 4.0e+2F*dt*dt*dt*u[t0][x + 2][y + 2]/r0;
}
}
gettimeofday(&end_section0, NULL);
timers->section0 += (double)(end_section0.tv_sec-start_section0.tv_sec)+(double)(end_section0.tv_usec-start_section0.tv_usec)/1000000;
struct timeval start_section1, end_section1;
gettimeofday(&start_section1, NULL);
for (int p_src = p_src_m; p_src <= p_src_M; p_src += 1)
{
//source injection
//...
}
gettimeofday(&end_section1, NULL);
timers->section1 += (double)(end_section1.tv_sec-start_section1.tv_sec)+(double)(end_section1.tv_usec-start_section1.tv_usec)/1000000;
struct timeval start_section2, end_section2;
gettimeofday(&start_section2, NULL);
for (int p_rec = p_rec_m; p_rec <= p_rec_M; p_rec += 1)
{
//receivers interpolation
//...
}
gettimeofday(&end_section2, NULL);
timers->section2 += (double)(end_section2.tv_sec-start_section2.tv_sec)+(double)(end_section2.tv_usec-start_section2.tv_usec)/1000000;
}
return 0;
}op2’s C code (differences are highlighted by //<<<<<<<<<<<<<<<<<<<<):
// #define's
//...
// declare dataobj struct
//...
// declare profiler struct
//...
int Kernel(struct dataobj *restrict damp_vec, const float dt, struct dataobj *restrict m_vec, const float o_x, const float o_y, struct dataobj *restrict rec_vec, struct dataobj *restrict rec_coords_vec, struct dataobj *restrict src_vec, struct dataobj *restrict src_coords_vec, struct dataobj *restrict u_vec, struct dataobj *restrict usave_vec, const int x_M, const int x_m, const int y_M, const int y_m, const int p_rec_M, const int p_rec_m, const int p_src_M, const int p_src_m, const int time_M, const int time_m, struct profiler * timers)
{
// ...
// ...
float (*restrict u)[u_vec->size[1]][u_vec->size[2]] __attribute__ ((aligned (64))) = (float (*)[u_vec->size[1]][u_vec->size[2]]) u_vec->data;
//<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<DECLARE USAVE<<<<<<<<<<<<<<<<<<<<<
float (*restrict usave)[usave_vec->size[1]][usave_vec->size[2]] __attribute__ ((aligned (64))) = (float (*)[usave_vec->size[1]][usave_vec->size[2]]) usave_vec->data;
//<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
//flush denormal numbers...
for (int time = time_m, t0 = (time)%(3), t1 = (time + 1)%(3), t2 = (time + 2)%(3); time <= time_M; time += 1, t0 = (time)%(3), t1 = (time + 1)%(3), t2 = (time + 2)%(3))
{
struct timeval start_section0, end_section0;
gettimeofday(&start_section0, NULL);
for (int x = x_m; x <= x_M; x += 1)
{
#pragma omp simd
for (int y = y_m; y <= y_M; y += 1)
{
float r0 = 1.0e+4F*dt*m[x + 2][y + 2] + 5.0e+3F*(dt*dt)*damp[x + 1][y + 1];
u[t1][x + 2][y + 2] = 2.0e+4F*dt*m[x + 2][y + 2]*u[t0][x + 2][y + 2]/r0 - 1.0e+4F*dt*m[x + 2][y + 2]*u[t2][x + 2][y + 2]/r0 + 1.0e+2F*((dt*dt*dt)*u[t0][x + 1][y + 2]/r0 + (dt*dt*dt)*u[t0][x + 2][y + 1]/r0 + (dt*dt*dt)*u[t0][x + 2][y + 3]/r0 + (dt*dt*dt)*u[t0][x + 3][y + 2]/r0) + 5.0e+3F*(dt*dt)*damp[x + 1][y + 1]*u[t2][x + 2][y + 2]/r0 - 4.0e+2F*dt*dt*dt*u[t0][x + 2][y + 2]/r0;
}
}
gettimeofday(&end_section0, NULL);
timers->section0 += (double)(end_section0.tv_sec-start_section0.tv_sec)+(double)(end_section0.tv_usec-start_section0.tv_usec)/1000000;
//<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<SAVE SNAPSHOT<<<<<<<<<<<<<<<<<<<<<
if ((time)%(60) == 0)
{
struct timeval start_section1, end_section1;
gettimeofday(&start_section1, NULL);
for (int x = x_m; x <= x_M; x += 1)
{
#pragma omp simd
for (int y = y_m; y <= y_M; y += 1)
{
usave[time / 60][x + 2][y + 2] = u[t0][x + 2][y + 2];
}
}
//<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
gettimeofday(&end_section1, NULL);
timers->section1 += (double)(end_section1.tv_sec-start_section1.tv_sec)+(double)(end_section1.tv_usec-start_section1.tv_usec)/1000000;
}
struct timeval start_section2, end_section2;
gettimeofday(&start_section2, NULL);
for (int p_src = p_src_m; p_src <= p_src_M; p_src += 1)
{
//source injection
//...
}
gettimeofday(&end_section2, NULL);
timers->section2 += (double)(end_section2.tv_sec-start_section2.tv_sec)+(double)(end_section2.tv_usec-start_section2.tv_usec)/1000000;
struct timeval start_section3, end_section3;
gettimeofday(&start_section3, NULL);
for (int p_rec = p_rec_m; p_rec <= p_rec_M; p_rec += 1)
{
//receivers interpolation
//...
}
gettimeofday(&end_section3, NULL);
timers->section3 += (double)(end_section3.tv_sec-start_section3.tv_sec)+(double)(end_section3.tv_usec-start_section3.tv_usec)/1000000;
}
return 0;
}To inspect the full codes of op1 and op2, run the block below:
def print2file(filename, thingToPrint):
import sys
orig_stdout = sys.stdout
f = open(filename, 'w')
sys.stdout = f
print(thingToPrint)
f.close()
sys.stdout = orig_stdout
# print2file("op1.c", op1) # uncomment to print to file
# print2file("op2.c", op2) # uncomment to print to file
# print(op1) # uncomment to print here
# print(op2) # uncomment to print hereTo run snaps as a movie (outside Jupyter Notebook), run the code below, altering filename, nsnaps, nx, nz accordingly:
#NBVAL_IGNORE_OUTPUT
#NBVAL_SKIP
from IPython.display import HTML
import matplotlib.pyplot as plt
import matplotlib.animation as animation
filename = "naivsnaps.bin"
nsnaps = 100
fobj = open(filename, "rb")
snapsObj = np.fromfile(fobj, dtype=np.float32)
snapsObj = np.reshape(snapsObj, (nsnaps, vnx, vnz))
fobj.close()
fig, ax = plt.subplots()
matrice = ax.imshow(snapsObj[0, :, :].T, vmin=-1, vmax=1, cmap="seismic")
plt.colorbar(matrice)
plt.xlabel('x')
plt.ylabel('z')
plt.title('Modelling one shot over a 2-layer velocity model with Devito.')
def update(i):
matrice.set_array(snapsObj[i, :, :].T)
return matrice,
# Animation
ani = animation.FuncAnimation(fig, update, frames=nsnaps, interval=50, blit=True)
plt.close(ani._fig)
HTML(ani.to_html5_video())References
Louboutin, M., Witte, P., Lange, M., Kukreja, N., Luporini, F., Gorman, G., & Herrmann, F. J. (2017). Full-waveform inversion, Part 1: Forward modeling. The Leading Edge, 36(12), 1033-1036.