%matplotlib inline
shape = (101, 101)
extent = (2000., 2000.)
nbpml = 10 # Number of PMLs on each sideBoundary conditions tutorial
This tutorial aims to demonstrate how users can implement various boundary conditions in Devito, building on concepts introduced in previous tutorials. Over the course of this notebook we will go over the implementation of both free surface boundary conditions and perfectly-matched layers (PMLs) in the context of the first-order acoustic wave equation. This tutorial is based on a simplified version of the method outlined in Liu and Tao’s 1997 paper (https://doi.org/10.1121/1.419657).
We will set up our domain with PMLs along the left, right, and bottom edges, and free surface boundaries at the top as shown below.
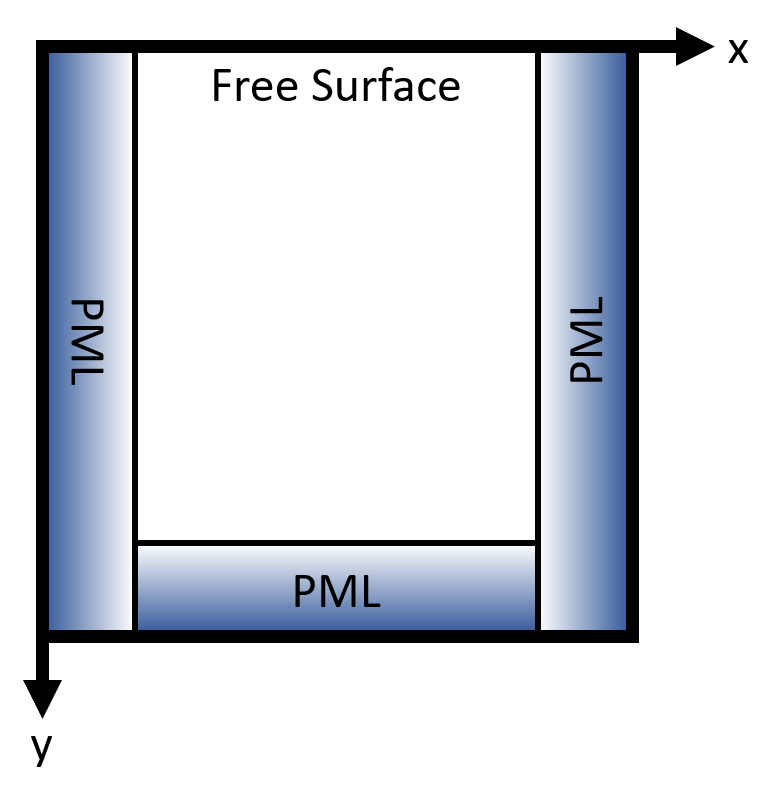
Note that whilst in practice we would want the PML tapers to overlap in the corners, this requires additional subdomains. As such, they are omitted for simplicity.
As always, we will begin by specifying some parameters for our Grid:
We will need to use subdomains to accomodate the modified equations in the PML regions. As Grid objects cannot have subdomains added retroactively, we must define our subdomains beforehand.
from devito import SubDomain
s_o = 6 # Space order
class MainDomain(SubDomain): # Main section with no damping
name = 'main'
def __init__(self, PMLS, S_O):
super().__init__()
self.PMLS = PMLS
self.S_O = S_O
def define(self, dimensions):
x, y = dimensions
return {x: ('middle', self.PMLS, self.PMLS),
y: ('middle', self.S_O//2, self.PMLS)}
class Left(SubDomain): # Left PML region
name = 'left'
def __init__(self, PMLS):
super().__init__()
self.PMLS = PMLS
def define(self, dimensions):
x, y = dimensions
return {x: ('left', self.PMLS), y: y}
class Right(SubDomain): # Right PML region
name = 'right'
def __init__(self, PMLS):
super().__init__()
self.PMLS = PMLS
def define(self, dimensions):
x, y = dimensions
return {x: ('right', self.PMLS), y: y}
class Base(SubDomain): # Base PML region
name = 'base'
def __init__(self, PMLS):
super().__init__()
self.PMLS = PMLS
def define(self, dimensions):
x, y = dimensions
return {x: ('middle', self.PMLS, self.PMLS), y: ('right', self.PMLS)}
class FreeSurface(SubDomain): # Free surface region
name = 'freesurface'
def __init__(self, PMLS, S_O):
super().__init__()
self.PMLS = PMLS
self.S_O = S_O
def define(self, dimensions):
x, y = dimensions
return {x: ('middle', self.PMLS, self.PMLS), y: ('left', self.S_O//2)}
main_domain = MainDomain(nbpml, s_o)
left = Left(nbpml)
right = Right(nbpml)
base = Base(nbpml)
freesurface = FreeSurface(nbpml, s_o)And create the grid, attaching our subdomains:
from devito import Grid
grid = Grid(shape=shape, extent=extent,
subdomains=(main_domain, left, right, base, freesurface))
x, y = grid.dimensionsWe can then begin to specify our problem starting with some parameters.
density = 1. # 1000kg/m^3
velocity = 4. # km/s
gamma = 0.0002 # Absorption coefficientWe also need a TimeFunction object for each of our wavefields. As particle velocity is a vector, we will choose a VectorTimeFunction object to encapsulate it.
from devito import TimeFunction, VectorTimeFunction, NODE
p = TimeFunction(name='p', grid=grid, time_order=1,
space_order=s_o, staggered=NODE)
v = VectorTimeFunction(name='v', grid=grid, time_order=1,
space_order=s_o)A VectorTimeFunction is near identical in function to a standard TimeFunction, albeit with a field for each grid dimension. The fields associated with each component can be accessed as follows:
print(v[0].data) # Print the data attribute associated with the x component of v[[[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
...
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]]
[[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
...
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]]]You may have also noticed the keyword staggered in the arguments when we created these functions. As one might expect, these are used for specifying where derivatives should be evaluated relative to the grid, as required for implementing formulations such as the first-order acoustic wave equation or P-SV elastic. Passing a function staggered=NODE specifies that its derivatives should be evaluated at the node. One can also pass staggered=x or staggered=y to stagger the grid by half a spacing in those respective directions. Additionally, a tuple of dimensions can be passed to stagger in multiple directions (e.g. staggered=(x, y)). VectorTimeFunction objects have their associated grids staggered by default.
We will also need to define a field for integrating pressure over time:
p_i = TimeFunction(name='p_i', grid=grid, time_order=1,
space_order=1, staggered=NODE)Next we prepare the source term:
import numpy as np
from examples.seismic import TimeAxis, RickerSource
t0 = 0. # Simulation starts at t=0
tn = 400. # Simulation length in ms
dt = 1e2*(1. / np.sqrt(2.)) / 60. # Time step
time_range = TimeAxis(start=t0, stop=tn, step=dt)
f0 = 0.02
src = RickerSource(name='src', grid=grid, f0=f0,
npoint=1, time_range=time_range)
# Position source centrally in all dimensions
src.coordinates.data[0, :] = 1000.src.show()
For our PMLs, we will need some damping parameter. In this case, we will use a quadratic taper over the absorbing regions on the left and right sides of the domain.
# Damping parameterisation
d_l = (1-0.1*x)**2 # Left side
d_r = (1-0.1*(grid.shape[0]-1-x))**2 # Right side
d_b = (1-0.1*(grid.shape[1]-1-y))**2 # Base edgeNow for our main domain equations:
from devito import Eq, grad, div
eq_v = Eq(v.forward, v - dt*grad(p)/density,
subdomain=grid.subdomains['main'])
eq_p = Eq(p.forward, p - dt*velocity**2*density*div(v.forward),
subdomain=grid.subdomains['main'])We will also need to set up p_i to calculate the integral of p over time for out PMLs:
eq_p_i = Eq(p_i.forward, p_i + dt*(p.forward+p)/2)And add the equations for our damped region:
# Left side
eq_v_damp_left = Eq(v.forward,
(1-d_l)*v - dt*grad(p)/density,
subdomain=grid.subdomains['left'])
eq_p_damp_left = Eq(p.forward,
(1-gamma*velocity**2*dt-d_l*dt)*p
- d_l*gamma*velocity**2*p_i
- dt*velocity**2*density*div(v.forward),
subdomain=grid.subdomains['left'])
# Right side
eq_v_damp_right = Eq(v.forward,
(1-d_r)*v - dt*grad(p)/density,
subdomain=grid.subdomains['right'])
eq_p_damp_right = Eq(p.forward,
(1-gamma*velocity**2*dt-d_r*dt)*p
- d_r*gamma*velocity**2*p_i
- dt*velocity**2*density*div(v.forward),
subdomain=grid.subdomains['right'])
# Base edge
eq_v_damp_base = Eq(v.forward,
(1-d_b)*v - dt*grad(p)/density,
subdomain=grid.subdomains['base'])
eq_p_damp_base = Eq(p.forward,
(1-gamma*velocity**2*dt-d_b*dt)*p
- d_b*gamma*velocity**2*p_i
- dt*velocity**2*density*div(v.forward),
subdomain=grid.subdomains['base'])We next add our free surface boundary conditions. Note that this implementation is based off that found in examples/seismic/acoustic/operators.py.
from devito import sign, norm
from devito.symbolics import retrieve_functions, INT
def free_surface_top(eq, subdomain, update):
"""
Modify a stencil such that it is folded back on
itself rather than leaving the model domain. This is
achieved by replacing the symbolic indices for some
function of those indices. Depending on how this is
done, this can be used to implement a pressure or
velocity free-surface. This is the MPI-safe method
of implementing a free-surface boundary condition
in Devito.
Parameters
----------
eq : Eq
The update stencil to modify
subdomain : FreeSurface
The subdomain in which the modification is
applied
update : str
The field being updated: 'pressure' or 'velocity'
"""
lhs, rhs = eq.evaluate.args
# Get vertical subdimension and its parent
yfs = subdomain.dimensions[-1]
y = yfs.parent
# Functions present in stencil
funcs = retrieve_functions(rhs)
mapper = {}
for f in funcs:
# Get the y index
yind = f.indices[-1]
if (yind - y).as_coeff_Mul()[0] < 0:
# If point position in stencil is negative
# Substitute the dimension for its subdomain companion
# Get the symbolic sign of this
s = sign(yind.subs({y: yfs, y.spacing: 1}))
if update == 'velocity':
# Antisymmetric mirror
# Substitute where index is negative for -ve where index is positive
mapper.update({f: s*f.subs({yind: INT(abs(yind))})})
elif update == 'pressure':
# Symmetric mirror
# Substitute where index is negative for +ve where index is positive
mapper.update({f: f.subs({yind: INT(abs(yind))})})
return Eq(lhs, rhs.subs(mapper), subdomain=subdomain)
fs_p = free_surface_top(eq_p, grid.subdomains['freesurface'], 'pressure')
fs_v = free_surface_top(eq_v, grid.subdomains['freesurface'], 'velocity')And our source terms:
src_term = src.inject(field=p.forward, expr=src)Construct our operator and run:
from devito import Operator
op = Operator([eq_v, fs_v, eq_v_damp_left, eq_v_damp_base, eq_v_damp_right,
eq_p, fs_p, eq_p_damp_left, eq_p_damp_base, eq_p_damp_right,
eq_p_i]
+ src_term)
op(time=time_range.num-1)Operator `Kernel` ran in 0.05 sPerformanceSummary([(PerfKey(name='section0', rank=None),
PerfEntry(time=4.9e-05, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section1', rank=None),
PerfEntry(time=0.0036749999999999908, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section2', rank=None),
PerfEntry(time=0.013221000000000004, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section3', rank=None),
PerfEntry(time=0.0037539999999999913, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section4', rank=None),
PerfEntry(time=0.013060000000000006, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section5', rank=None),
PerfEntry(time=0.003929000000000017, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[])),
(PerfKey(name='section6', rank=None),
PerfEntry(time=0.003147999999999996, gflopss=0.0, gpointss=0.0, oi=0.0, ops=0, itershapes=[]))])It is important to remember that the ordering of equations when an Operator is created dictates the order of loops within the generated c code. As such, the v equations all need to be placed before the p ones otherwise the operator will attempt to use the updated v fields before they have been updated.
Now let’s plot the wavefield.
import matplotlib.pyplot as plt
scale = np.max(p.data[1])
plt.imshow(p.data[1].T/scale,
origin="upper",
vmin=-1, vmax=1,
extent=[0, grid.extent[0], grid.extent[1], 0],
cmap='seismic')
plt.colorbar()
plt.xlabel("x (m)")
plt.ylabel("y (m)")
plt.show()
As we can see, the wave is effectively damped at the edge of the domain by the 10 layers of PMLs, with diminished reflections back into the domain.
assert(np.isclose(norm(v[0]), 0.1955, atol=0, rtol=1e-4))
assert(np.isclose(norm(v[1]), 0.4596, atol=0, rtol=1e-4))
assert(np.isclose(norm(p), 2.0043, atol=0, rtol=1e-4))